Perkalian Matriks dengan Bahasa Pascal
Bismillah,
Mungkin banyak yang terheran mengapa masih saja ada tulisan tentang Bahasa Pascal, bahkan bisa jadi berpikir, kok Pascal sih? he…he… Iya, betul, Bahasa Pascal, Bahasa Pemprograman ini banyak digunakan sebagai bahasa pengantar untuk mata kuliah algoritma.
Jangan takut belajar bahasa ini, karena seorang software developer memerlukan skill algoritma yang baik, maka pemahaman akan bahasa Pascal di masa awal tumbuh kembang sebagai software developer akan terasa manfaat nya di masa yang akan datang, InsyaAllah.
Dibawah ini adalah program untuk melakukan operasi pada matriks. Sengaja tidak saya jelaskan secara rinci per baris source code nya, agar pembaca bisa menelaah sendiri ke buku-buku yang memang mengajarkan Bahasa Pascal.
Saat saya kuliah dulu, di ajarkan mata kuliah Matematika Teknik dan Pemprograman I, nah, ketika belajar matriks di Matematika Teknik, saya coba terapkan ilmu yang saya dapat dari maka kuliah Pemprograman I.
Kepada para adik-adik mahasiswa jurusan IT, tetap jawab soal matriks secara manual ya, jangan pakai program ini, karena itu melatih kejujuran kalian, he…he…
Cara compile program pascal di Linux
Disini saya contohkan penggunaan Free Pascal Compiler:
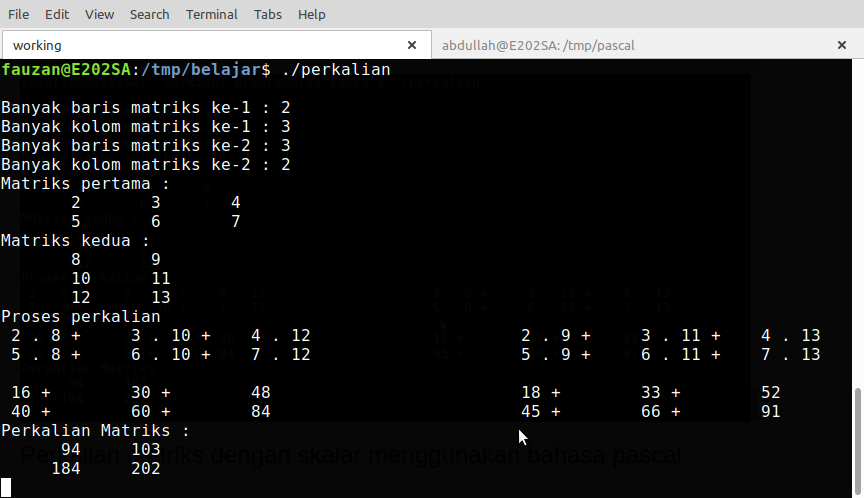
Perkalian 2 buah matriks menggunakan bahasa Pascal
program perkalian_matriks;
uses crt;
var
M1 : array[1..20, 1..20] of longint;
M2 : array[1..20, 1..20] of longint;
M3 : array[1..20, 1..20] of longint;
n : array[1..2] of integer;
m : array[1..2] of integer;
i, j, x, y, k, l : integer;
begin
clrscr;
for k := 1 to 2 do begin
write('Banyak baris matriks ke-', k, ' : ');
readln(m[k]);
write('Banyak kolom matriks ke-', k, ' : ');
readln(n[k]);
end;
if (n[1] <> m[2]) then
writeln('Tidak bisa dikalikan!')
else begin
writeln('Matriks pertama : ');
y := 6;
for i := 1 to m[1] do begin
x := 8;
for j := 1 to n[1] do begin
gotoxy(x,y);
readln(M1[i,j]);
x := x + 8;
end;
y := y + 1;
end;
writeln('Matriks kedua : ');
y := y + 1;
for i := 1 to m[2] do begin
x := 8;
for j := 1 to n[2] do begin
gotoxy(x,y);
readln(M2[i,j]);
x := x + 8;
end;
y := y + 1;
end;
writeln('Proses perkalian');
y := y + 1;
for i := 1 to m[1] do begin
x := 2;
for j := 1 to n[2] do begin
M3[i,j] := 0;
for l := 1 to n[1] do begin;
M3[i,j] := M3[i,j] + (M1[i,l] * M2[l,j]);
gotoxy(x,y);
write(M1[i,l], ' . ', M2[l,j]);
if l < n[1] then begin
write(' + ');
end;
x := x + 12;
end;
x := x + 15;
end;
y := y + 1;
end;
y := y + 1;
for i := 1 to m[1] do begin
x := 2;
for j := 1 to n[2] do begin
for l := 1 to n[1] do begin;
gotoxy(x,y);
write(M1[i,l] * M2[l,j]);
if l < n[1] then begin
write(' + ');
end;
x := x + 12;
end;
x := x + 15;
end;
y := y + 1;
end;
writeln;
writeln('Perkalian Matriks : ');
for i := 1 to m[1] do begin
for j := 1 to n[2] do
write(M3[i,j]:8);
writeln;
end;
end;
readln;
end.Contoh:
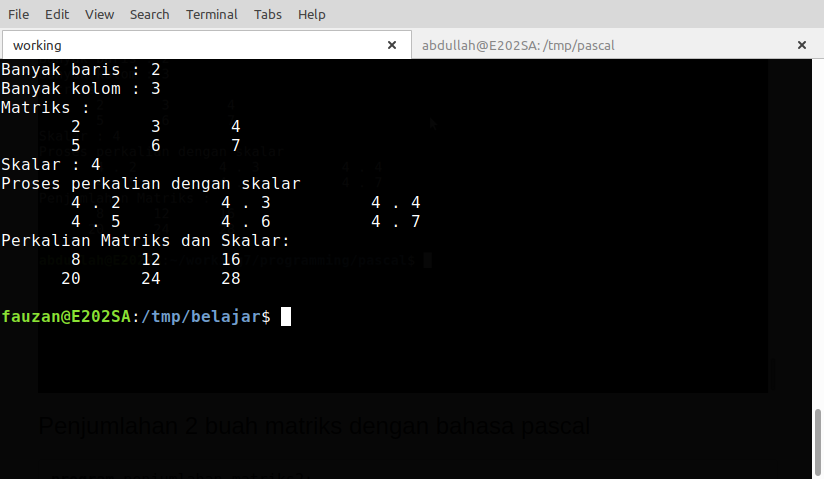
Perkalian matriks dengan skalar menggunakan bahasa pascal
program perkalian_matriks_dg_skalar;
uses crt;
var
M1 : array[1..20, 1..20] of integer;
M2 : array[1..20, 1..20] of integer;
i, j, m, n, x, y, s : integer;
begin
clrscr;
write('Banyak baris : ');
readln(m);
write('Banyak kolom : ');
readln(n);
writeln('Matriks : ');
y := 4;
for i := 1 to m do begin
x := 8;
for j := 1 to n do begin
gotoxy(x,y);
readln(M1[i,j]);
x := x + 8;
end;
y := y + 1;
end;
write('Skalar : ');
readln(s);
writeln('Proses perkalian dengan skalar');
y := 6 + m;
for i := 1 to m do begin
x := 8;
for j := 1 to n do begin
M2[i,j] := s * M1[i,j];
gotoxy(x,y);
write(s, ' . ', M1[i,j]);
x := x + 15;
end;
y := y + 1;
end;
writeln;
writeln('Perkalian Matriks dan Skalar: ');
for i := 1 to m do begin
for j := 1 to n do
write(M2[i,j]:8);
writeln;
end;
readln;
end.Contoh:
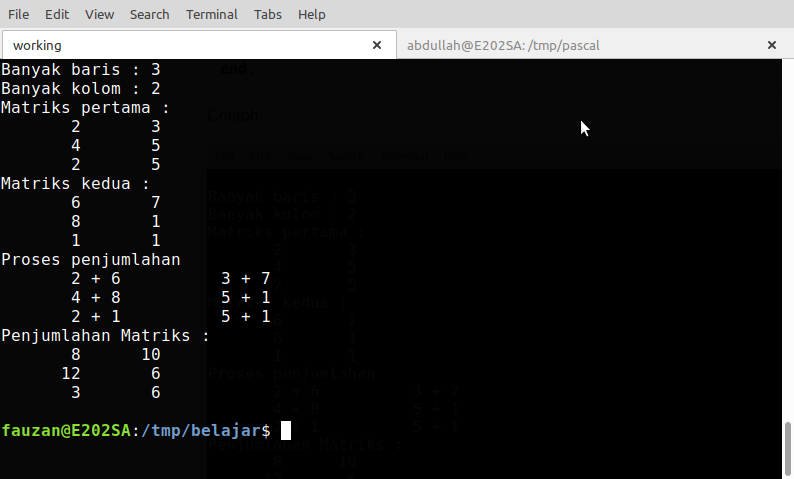
Penjumlahan 2 buah matriks dengan bahasa pascal
program penjumlahan_matriks2;
uses crt;
var
M1 : array[1..20, 1..20] of integer;
M2 : array[1..20, 1..20] of integer;
M3 : array[1..20, 1..20] of integer;
i, j, m, n, x, y : integer;
begin
clrscr;
write('Banyak baris : ');
readln(m);
write('Banyak kolom : ');
readln(n);
writeln('Matriks pertama : ');
y := 4;
for i := 1 to m do begin
x := 8;
for j := 1 to n do begin
gotoxy(x,y);
readln(M1[i,j]);
x := x + 8;
end;
y := y + 1;
end;
writeln('Matriks kedua : ');
y := 5 + m;
for i := 1 to m do begin
x := 8;
for j := 1 to n do begin
gotoxy(x,y);
readln(M2[i,j]);
x := x + 8;
end;
y := y + 1;
end;
writeln('Proses penjumlahan');
y := 6 + (2 * m);
for i := 1 to m do begin
x := 8;
for j := 1 to n do begin
M3[i,j] := M1[i,j] + M2[i,j];
gotoxy(x,y);
write(M1[i,j], ' + ', M2[i,j]);
x := x + 15;
end;
y := y + 1;
end;
writeln;
writeln('Penjumlahan Matriks : ');
for i := 1 to m do begin
for j := 1 to n do
write(M3[i,j]:8);
writeln;
end;
readln;
end.Contoh:
Pengurangan 2 buah matriks dengan bahasa pascal
program pengurangan_matriks2;
uses crt;
var
M1 : array[1..20, 1..20] of integer;
M2 : array[1..20, 1..20] of integer;
M3 : array[1..20, 1..20] of integer;
i, j, m, n, x, y : integer;
begin
clrscr;
write('Banyak baris : ');
readln(m);
write('Banyak kolom : ');
readln(n);
writeln('Matriks pertama : ');
y := 4;
for i := 1 to m do begin
x := 8;
for j := 1 to n do begin
gotoxy(x,y);
readln(M1[i,j]);
x := x + 8;
end;
y := y + 1;
end;
writeln('Matriks kedua : ');
y := 5 + m;
for i := 1 to m do begin
x := 8;
for j := 1 to n do begin
gotoxy(x,y);
readln(M2[i,j]);
x := x + 8;
end;
y := y + 1;
end;
writeln('Proses pengurangan');
y := 6 + (2 * m);
for i := 1 to m do begin
x := 8;
for j := 1 to n do begin
M3[i,j] := M1[i,j] - M2[i,j];
gotoxy(x,y);
write(M1[i,j], ' - ', M2[i,j]);
x := x + 15;
end;
y := y + 1;
end;
writeln;
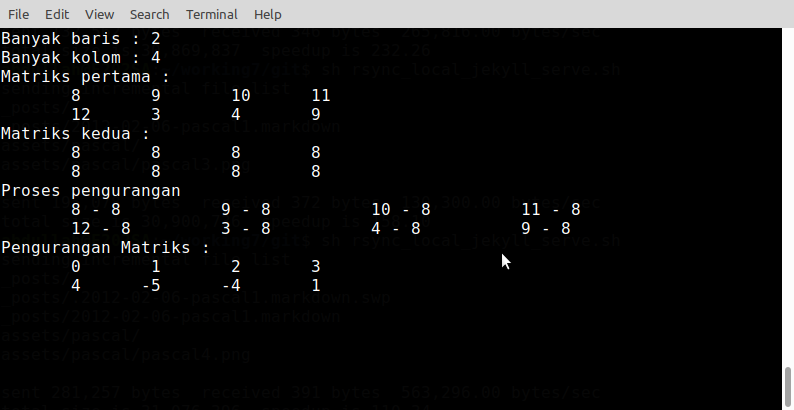
writeln('Pengurangan Matriks : ');
for i := 1 to m do begin
for j := 1 to n do
write(M3[i,j]:8);
writeln;
end;
readln;
end.Contoh:
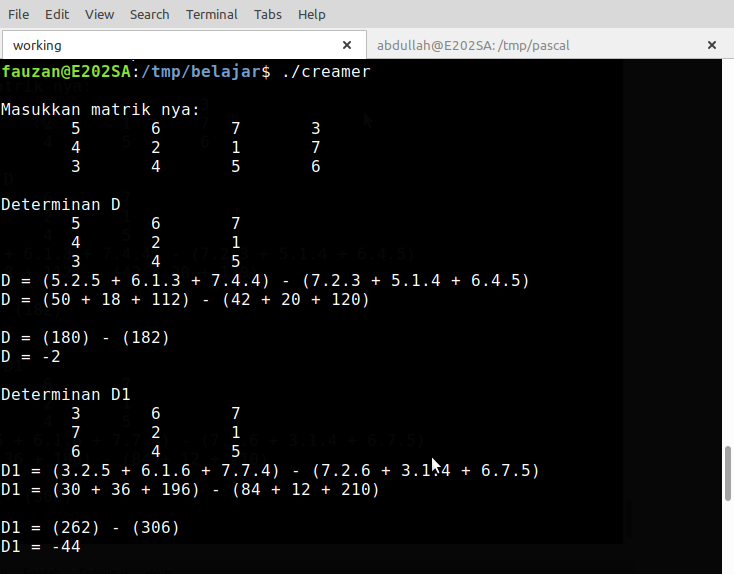
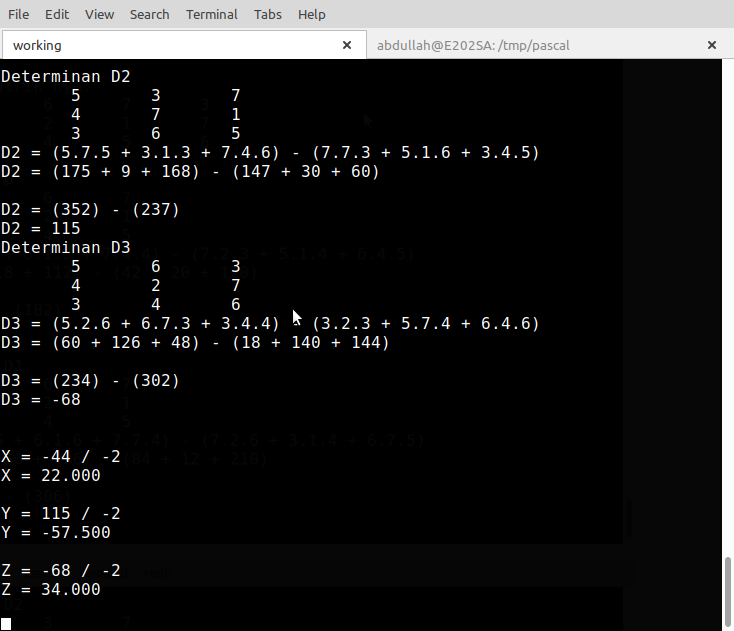
Penyelesaian persamaan linear dengan metode crammer
Dibawah ini adalah contoh penyelesaain persamaan menggunakan metode crammer, saya tulis dalam pascal, walaupun saya dalam hati lebih cinta Bahasa C, he.. hee Semoga bermanfaat bagi para pemula yang belajar programming.
Di sini pascal memang sudah tidak umum lagi di dunia industri, tapi masih di ajarkan di kampus-kampus sebagai pengantar pelajaran algoritma. Jadi, yang penting paham algoritma dulu, apapun bahasa pengantar untuk itu.
jarak spasi dalam program ini 8 karakter? kenapa begitu? hee…he…, karena saya mengkompile nya di terminal di linux dengan FPC (Free Pascal Compiler), jadi masih tampil dengan indah di terminal saya. Adapun kalau di compile dengan turbo pascal atau compiler lain, maka tampilan hasilnya akan berantakan, he.. hee.. akhirnya, saran saya, gunakan fpc under linux!
{
program penyelesaian persamaan linear dengan metode crammer
algoritma:
1. Masukkan matrik persamaan
2. Hitung Determinan D
3. Xn = Dn / D
ditulis oleh: Muhamamd Muntaza
email : muhammad@muntaza.id
lisensi : GPL v3
}
program crammer_3var;
uses crt;
var
M : array[1..20, 1..20] of longint;
D : array[0..4] of integer;
soal : array[1..3] of real;
i, j, x, y : integer;
begin
clrscr;
writeln('Masukkan matrik nya: ');
y := 2;
for i := 1 to 3 do begin
x := 8;
for j := 1 to 4 do begin
gotoxy(x,y);
readln(M[i,j]);
x := x + 8;
end;
y := y + 1;
end;
writeln;
{Diterminan D}
writeln('Determinan D ');
for i := 1 to 3 do begin
for j := 1 to 3 do begin
write(M[i,j]:8);
end;
writeln;
end;
writeln ('D = (', M[1,1], '.', M[2,2], '.', M[3,3], ' + ',
M[1,2], '.', M[2,3], '.', M[3,1], ' + ',
M[1,3], '.', M[2,1], '.', M[3,2], ')',
' - ',
'(', M[1,3], '.', M[2,2], '.', M[3,1], ' + ',
M[1,1], '.', M[2,3], '.', M[3,2], ' + ',
M[1,2], '.', M[2,1], '.', M[3,3], ')');
writeln ('D = (', M[1,1] * M[2,2] * M[3,3], ' + ',
M[1,2] * M[2,3] * M[3,1], ' + ',
M[1,3] * M[2,1] * M[3,2], ')',
' - ',
'(', M[1,3] * M[2,2] * M[3,1], ' + ',
M[1,1] * M[2,3] * M[3,2], ' + ',
M[1,2] * M[2,1] * M[3,3], ')');
writeln;
writeln ('D = (', (M[1,1] * M[2,2] * M[3,3]) +
(M[1,2] * M[2,3] * M[3,1]) +
(M[1,3] * M[2,1] * M[3,2]), ')',
' - ',
'(', (M[1,3] * M[2,2] * M[3,1]) +
(M[1,1] * M[2,3] * M[3,2]) +
(M[1,2] * M[2,1] * M[3,3]), ')');
D[0] := (((M[1,1] * M[2,2] * M[3,3]) +
(M[1,2] * M[2,3] * M[3,1]) +
(M[1,3] * M[2,1] * M[3,2]))
-
((M[1,3] * M[2,2] * M[3,1]) +
(M[1,1] * M[2,3] * M[3,2]) +
(M[1,2] * M[2,1] * M[3,3])));
writeln ('D = ', D[0]);
{D1}
writeln;
writeln('Determinan D1 ');
for i := 1 to 3 do begin
for j := 1 to 3 do begin
if (j = 1) then
write(M[i,j+3]:8)
else
write(M[i,j]:8);
end;
writeln;
end;
writeln ('D1 = (', M[1,4], '.', M[2,2], '.', M[3,3], ' + ',
M[1,2], '.', M[2,3], '.', M[3,4], ' + ',
M[1,3], '.', M[2,4], '.', M[3,2], ')',
' - ',
'(', M[1,3], '.', M[2,2], '.', M[3,4], ' + ',
M[1,4], '.', M[2,3], '.', M[3,2], ' + ',
M[1,2], '.', M[2,4], '.', M[3,3], ')');
writeln ('D1 = (', M[1,4] * M[2,2] * M[3,3], ' + ',
M[1,2] * M[2,3] * M[3,4], ' + ',
M[1,3] * M[2,4] * M[3,2], ')',
' - ',
'(', M[1,3] * M[2,2] * M[3,4], ' + ',
M[1,4] * M[2,3] * M[3,2], ' + ',
M[1,2] * M[2,4] * M[3,3], ')');
writeln;
writeln ('D1 = (', (M[1,4] * M[2,2] * M[3,3]) +
(M[1,2] * M[2,3] * M[3,4]) +
(M[1,3] * M[2,4] * M[3,2]), ')',
' - ',
'(', (M[1,3] * M[2,2] * M[3,4]) +
(M[1,4] * M[2,3] * M[3,2]) +
(M[1,2] * M[2,4] * M[3,3]), ')');
D[1] := (((M[1,4] * M[2,2] * M[3,3]) +
(M[1,2] * M[2,3] * M[3,4]) +
(M[1,3] * M[2,4] * M[3,2]))
-
((M[1,3] * M[2,2] * M[3,4]) +
(M[1,4] * M[2,3] * M[3,2]) +
(M[1,2] * M[2,4] * M[3,3])));
writeln ('D1 = ', D[1]);
{D2}
writeln;
writeln('Determinan D2');
for i := 1 to 3 do begin
for j := 1 to 3 do begin
if (j = 2) then
write(M[i,j+2]:8)
else
write(M[i,j]:8);
end;
writeln;
end;
writeln ('D2 = (', M[1,1], '.', M[2,4], '.', M[3,3], ' + ',
M[1,4], '.', M[2,3], '.', M[3,1], ' + ',
M[1,3], '.', M[2,1], '.', M[3,4], ')',
' - ',
'(', M[1,3], '.', M[2,4], '.', M[3,1], ' + ',
M[1,1], '.', M[2,3], '.', M[3,4], ' + ',
M[1,4], '.', M[2,1], '.', M[3,3], ')');
writeln ('D2 = (', M[1,1] * M[2,4] * M[3,3], ' + ',
M[1,4] * M[2,3] * M[3,1], ' + ',
M[1,3] * M[2,1] * M[3,4], ')',
' - ',
'(', M[1,3] * M[2,4] * M[3,1], ' + ',
M[1,1] * M[2,3] * M[3,4], ' + ',
M[1,4] * M[2,1] * M[3,3], ')');
writeln;
writeln ('D2 = (', (M[1,1] * M[2,4] * M[3,3]) +
(M[1,4] * M[2,3] * M[3,1]) +
(M[1,3] * M[2,1] * M[3,4]), ')',
' - ',
'(', (M[1,3] * M[2,4] * M[3,1]) +
(M[1,1] * M[2,3] * M[3,4]) +
(M[1,4] * M[2,1] * M[3,3]), ')');
D[2] := (((M[1,1] * M[2,4] * M[3,3]) +
(M[1,4] * M[2,3] * M[3,1]) +
(M[1,3] * M[2,1] * M[3,4]))
-
((M[1,3] * M[2,4] * M[3,1]) +
(M[1,1] * M[2,3] * M[3,4]) +
(M[1,4] * M[2,1] * M[3,3])));
writeln ('D2 = ', D[2]);
{Diterminan D3}
writeln('Determinan D3 ');
for i := 1 to 3 do begin
for j := 1 to 3 do begin
if (j = 3) then
write(M[i,j+1]:8)
else
write(M[i,j]:8);
end;
writeln;
end;
writeln ('D3 = (', M[1,1], '.', M[2,2], '.', M[3,4], ' + ',
M[1,2], '.', M[2,4], '.', M[3,1], ' + ',
M[1,4], '.', M[2,1], '.', M[3,2], ')',
' - ',
'(', M[1,4], '.', M[2,2], '.', M[3,1], ' + ',
M[1,1], '.', M[2,4], '.', M[3,2], ' + ',
M[1,2], '.', M[2,1], '.', M[3,4], ')');
writeln ('D3 = (', M[1,1] * M[2,2] * M[3,4], ' + ',
M[1,2] * M[2,4] * M[3,1], ' + ',
M[1,4] * M[2,1] * M[3,2], ')',
' - ',
'(', M[1,4] * M[2,2] * M[3,1], ' + ',
M[1,1] * M[2,4] * M[3,2], ' + ',
M[1,2] * M[2,1] * M[3,4], ')');
writeln;
writeln ('D3 = (', (M[1,1] * M[2,2] * M[3,4]) +
(M[1,2] * M[2,4] * M[3,1]) +
(M[1,4] * M[2,1] * M[3,2]), ')',
' - ',
'(', (M[1,4] * M[2,2] * M[3,1]) +
(M[1,1] * M[2,4] * M[3,2]) +
(M[1,2] * M[2,1] * M[3,4]), ')');
D[3] := (((M[1,1] * M[2,2] * M[3,4]) +
(M[1,2] * M[2,4] * M[3,1]) +
(M[1,4] * M[2,1] * M[3,2]))
-
((M[1,4] * M[2,2] * M[3,1]) +
(M[1,1] * M[2,4] * M[3,2]) +
(M[1,2] * M[2,1] * M[3,4])));
writeln ('D3 = ', D[3]);
writeln;
writeln;
writeln ('X = ', D[1], ' / ', D[0]);
soal[1] := D[1] / D[0];
writeln ('X = ', soal[1]:5:3);
writeln;
writeln ('Y = ', D[2], ' / ', D[0]);
soal[2] := D[2] / D[0];
writeln ('Y = ', soal[2]:5:3);
writeln;
writeln ('Z = ', D[3], ' / ', D[0]);
soal[3] := D[3] / D[0];
writeln ('Z = ', soal[3]:5:3);
writeln;
readln;
end.Contoh:
Alhamdulillah
Update 21 September 2021:
- Penambahan gambar contoh program saat di jalankan.
- Penggunaan Sub Judul dengan huruf yang lebih besar.
Daftar Pustaka:
- Utami, Ema, Dan kawan-kawan. 2007. Struktur Data Konsep & Implementasinya dalam Bahasa C & Free Pascal di GNU/LINUX. Jogjakarta: Graha Ilmu.
- Salim, Yeffriansjah. 2011. Modul Praktek Pemprograman Pascal. Banjarmasin: STMIK Indonesia Banjarmasin